Simulations numériques |
Ces modélisations ont été réalisées au laboratoire LEPA de l'Ecole Polytechnique Fédérale de Lausanne (EPFL) avec le logiciel Flux-Expert (thèses pour les biotechnologies, avec une dominante microfluidique, électrochimie et magnétisme). Les simulations pour l'industrie sont en page références.
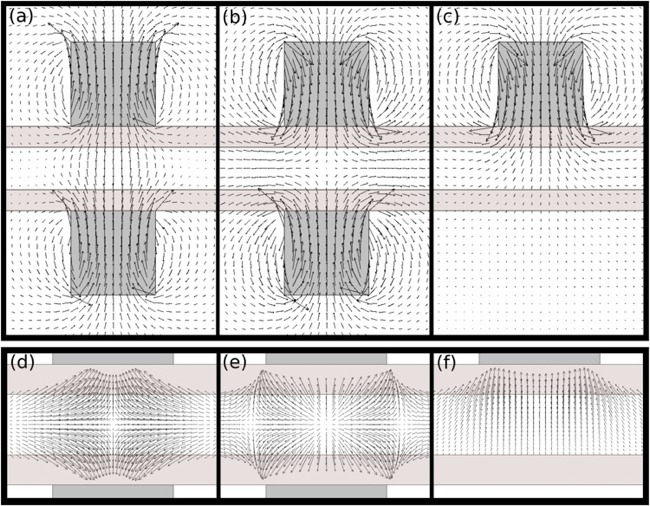
Aimants permanents pour la capture de billes magnétiques en microsystèmes (mode statique sans écoulement). Vecteurs lignes de champ magnétique (ligne du haut) et vecteurs force magnétique (ligne du bas) pour des aimants permanents rectangulaires placés de part et d'autre d'un microcanal (hauteur 100 microns).
Configuration d'attraction (1ère colonne) : billes piégées au centre.
Configuration de répulsion (2ème colonne) : billes piégées à l'entrée et à la sortie de la zone aimantée.
Configuration de"single magnet" (3ème colonne) : billes piégées sur le haut. Voir la description détaillée
(avec vérification expérimentale par visualisations) dans la publication suivante :
Magnetic forces produced by rectangular permanent magnets in static microsystems. Anne-Laure Gassner, M Abonnenc, H-X Chen, J Morandini, J Josserand, J S Rossier, J-M Busnel, and H.H. Girault - Lab on a Chip , volume 9, number 16, 2009.
______________
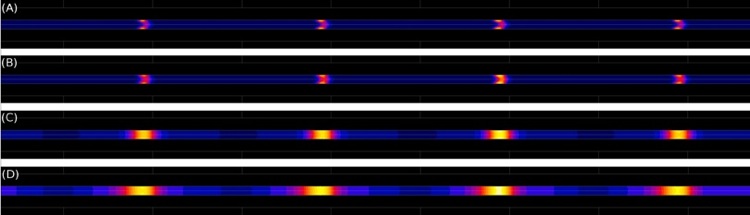
Capture de billes magnétiques en capillaire, par des aimants annulaires coaxiaux (avec modèle intégrant la microfluidique du fluide). Cette figure présente les isovaleurs de la concentration des billes dans un capillaire de 100 microns de diamètre, placé dans un collier d'aimants permanents annulaires : influence du coefficient de diffusion des billes sur la largeur des amas stabilisés, pour une vitesse d'écoulement de 1mm/s. L'immobilisation "multiplug" des billes est réalisée en créant un "collier" d'aimants annulaires espacés dont les polarités sont alternées. Cette simulation montre que la proximité entre les aimants et le capillaire permet d'augmenter fortement la force magnétique par rapport aux dispositifs classiques. Le débit de la solution peut alors être augmenté pour un même niveau de capture. Le modèle numérique est réalisé en deux temps : calcul de la distribution de force magnétique qui est ensuite injectée dans le calcul de convection-diffusion des billes (ici prises en compte comme une concentration d'espèces qui n'interagissent pas entre elles). Description complète dans la référence suivante, avec confirmation par visualisations au microscope :
Ring magnets for Magnetic Beads Trapping in a Capillary. Anne-Laure Gassner, J. Morandini, J. Josserand, H.H. Girault, Analytical Methods, vol. 3, 2011.______________

Optimisation de la capture de billes en microcanal par ajout de pistes magnétiques. Isovaleurs du champ magnétique vertical pour deux aimants permanents rectangulaires placés de part et d'autre d'un microcanal (A). Effet de la canalisation du champ magnétique par les pistes magnétiques (figure B), qui permettent de piéger les billes tout au long des aimants (et non seulement au centre), en créant des amas de billes de type "multiplug". L'augmentation de la quantité de billes capturées est confirmée par les visualisations de la publication ci-dessous, en accord avec les simulations numériques (figure ci-dessus, A-L Gassner) qui montrent que l'augmentation de la force magnétique permet de capturer les billes à plus haut débit de fluide.
Magnetic track array for efficient bead capture in microchannels. Mélanie Abonnenc, A-L Gassner, J Morandini, J Josserand, and H.H. Girault - Analytical and Bioanalytical Chemistry, volume 395, 2009.
______________
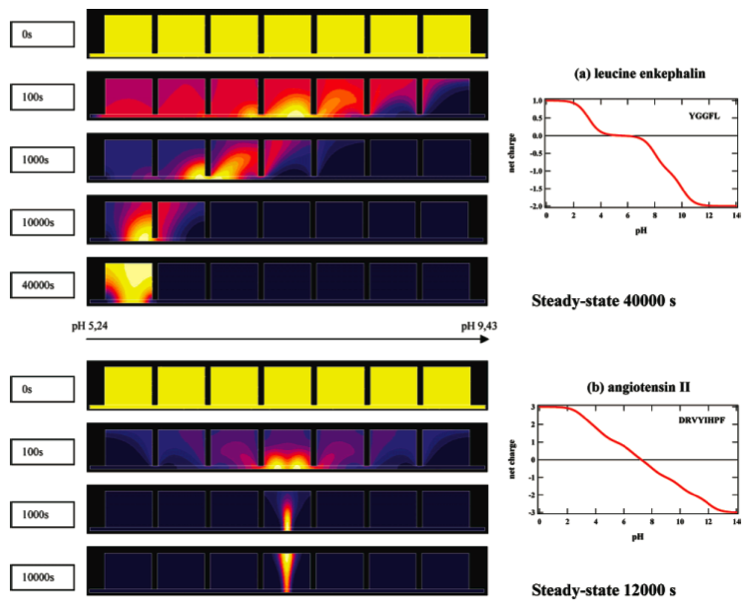
Fractionation de peptides par focalisation isoélectrique (IEF) dans une cellule Off-Gel. Cette figure montre l'évolution de la concentration des peptides dans une cellule Off-gel à 7 compartiments. La hauteur de la cellule est de 5mm. Le gel (zone du bas) assure la jonction entre les cellules uniformément concentrées en peptides au départ (condition initiale de 1 mM). Ce gel assure une gamme de pH de 5 à 9, soit un gradient de 0.8 unités pH/cm. Sous l'influence du champ électrique appliqué (100V/cm), les peptides migrent vers la zone de pH correspondant à leur pI (point isoélectrique de neutralité) et se focalisent dans cette zone. Cette simulation montre l'importance de bien connaître les courbes charge/pH des peptides (et surtout leur pente à la zone de pI, figures de droite) pour évaluer le temps de focalisation ainsi que sa qualité. Autres exemples de focalisations dans la référence ci-dessous :
Modeling the Isoelectric Focusing of Peptides in an OFFGEL Multicompartment Cell.
Hoang-Trang Lam, J. Josserand, N. Lion, and H. H. Girault - Journal of Proteome Research, volume 6, 2007.
______________
Mélange et réaction dans un écoulement microfluidique à 3 entrées. Ce mélangeur diffusif à 3 entrées, très simple de conception, met à profit le profil parabolique de vitesse du fluide pour augmenter le taux d’avancement de la réaction chimique (A+B->C) pour une longeur donnée du microcanal. En introduisant les espèces les moins diffusives (A) sur les bords du canal (configuration ABA), la réaction reste localisée sur les zones latérales à faible vitesse du fluide, et profitent alors d’un plus grand temps de résidence pour se réaliser. Pour la simulation ici représentée (illustrant les isovaleurs du produit de la réaction C), l’optimisation apporte un gain de 60% (ABA versus BAB). Ce gain peut atteindre un facteur 3 en réduisant le ratio des vitesses d’entrées VA/VB. Sur la droite, le profil de concentration du produit de réaction C est représenté en grisé. Le ratio des coefficients de diffusion DB/DA est ici de 10. Plus d'informations sur :
Sandwich mixer–reactor: influence of the diffusion coefficient and flow rate ratios.
Mélanie Abonnenc, J Josserand, and H H Girault - Lab on a Chip, volume 9, page 440–448, 2009.
______________
Adsoption dynamique de protéines en microcanal : comparaison du régime d'écoulement "stop flow" par rapport à l'écoulement continu. Cette étude montre dans quelles conditions le régime "stop-flow" (incubations successives des protéines) peut être préférable au régime d'écoulement continu, en se basant sur des critères de consommation minimum de protèines et d'uniformité de la couche adsorbée. Ce travail montre l'importance cruciale d'un bon choix de la vitesse d'écoulement pour un chargement en continu. Des formules sont données pour choisir la vitesse optimale en fonction des autres paramètres, incluant un nouveau paramètre adimensionnel. Ce modèle numérique tient compte du couplage entre la convection-diffusion des espèces et leur réaction d'adsorption à la paroi selon une cinétique de Langmuir. Description complète sur :
Dynamic protein adsorption in microchannels by "stop-flow" and continuous flow.
Andréa Lionello, J. Josserand, H. Jensen, and H. H. Girault - Lab Chip, volume 5, 2005.
______________
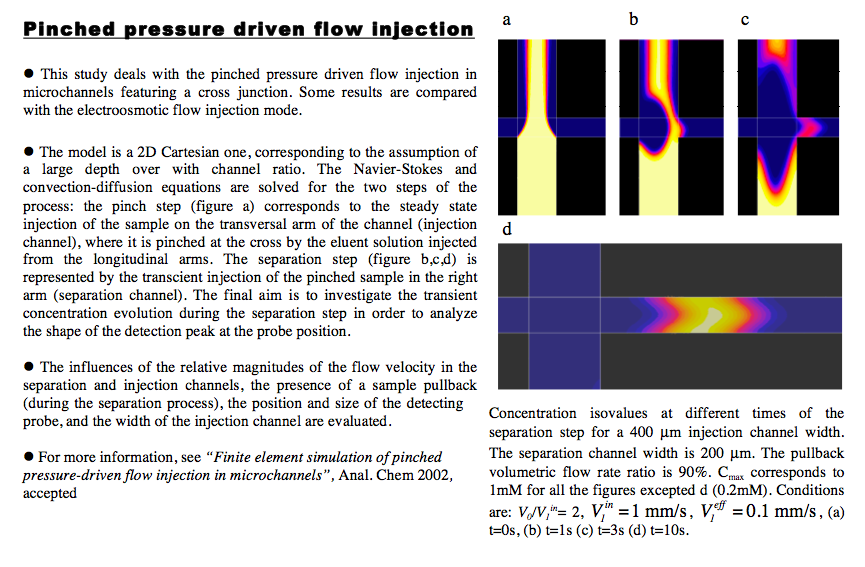
Injection de fluide en microcanal (écoulement de pression). Ce mode d’injection de type pincé se fait en 2 temps : injection de l’échantillon dans le canal vertical (a) puis séparation dans le canal horizontal (b,c,d). Ce mode d’injection permet de mnimiser la trainée du plug réalisé en créant un refoulement de l’échantillon dans le canal vertical (b,c). Ceci permet d’optimiser la qualité du pic de détection des espèces (capteur placé sur la droite). Parmi les différents paramètres évalués, il apparaît qu’un largeur minimum de plug doit être respectée pour minimiser les effets de tassement du pic de détection par la diffusion (pour un temps de passage donné entre l’injecteur et le capteur). Ceci explique la plus grande largeur du canal d’injection de la simulation (400 microns) par rapport au canal de séparation (200 microns). Des comparaisons sont réalisées par rapport à l'écoulement de type électro-osmotique (EOF flow).
Finite Element Simulation of Pinched Pressure-Driven Flow Injection in Microchannels.
Xiaoxia Bai, J. Josserand, H. Jensen, J. S. Rossier, and H. H. Girault - Analytical Chemistry, volume 74, 2002.______________
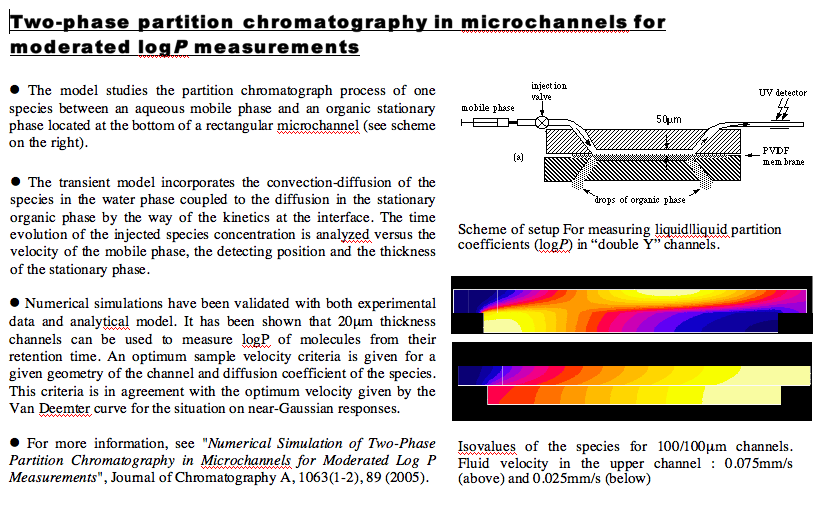
Numerical Simulation of Two-Phase Partition Chromatography in Microchannels. Sorina Ulmeanu,
J. Josserand, H. Jensen, G. Bouchard, P.-A. Carrupt, and H. H. Girault Journal of Chromatography A, vol 1063, 2005.
______________
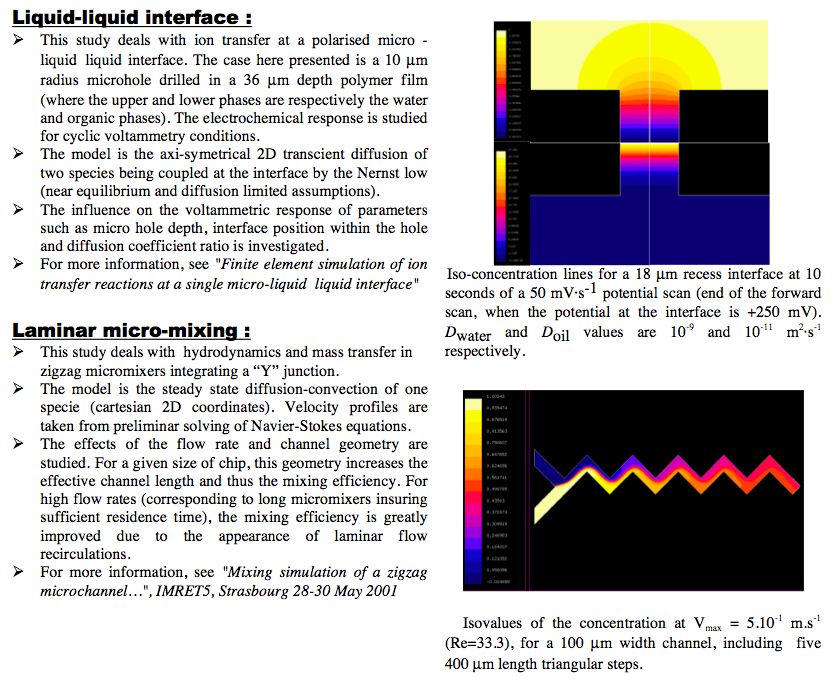
Finite Element Simulation of Ion Transfer Reactions at a Single Micro-Liquid/Liquid Interface.
J. Josserand, J. Morandini, H. J. Lee, R. Ferrigno, and H. H. Girault - J. Electroanal. Chem, volume 468, 1999.
Mixing Processes in a Zigzag Microchannel: Finite Element Simulations and Optical Study.
Virginie Mengeaud, J. Josserand, and H. H. Girault In Analytical Chemistry, volume 74, number 16, 2002.
______________

Numerical Investigation of an Electrochemically Induced Tagging in a Nanospray for Protein
Analysis. Tatiana Rohner, J. Josserand, H. Jensen, and H. H. Girault - Analytical Chemistry, volume 75, 2003.
______________
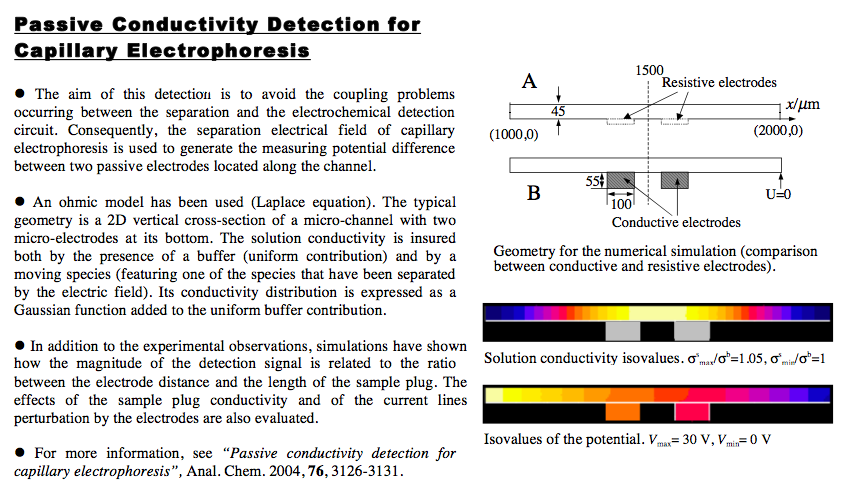
Passive Conductivity Detection for Capillary Electrophoresis. Xiaoxia Bai, Z. Wu, J. Josserand,
H. Jensen, H. Schafer, and H. H. Girault - Analytical Chemistry, volume 76, number 11, 2004.
______________
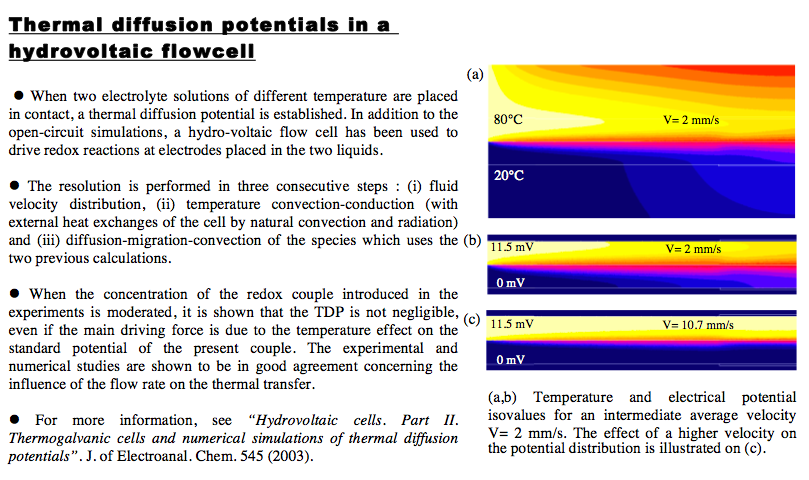
Hydrovoltaic cells. Part II: Thermogalvanic cells and numerical simulations of thermal diffusion potentials. J. Josserand, V. Devaud, H. G. Lagger, and H. H. Girault - Journal of Electroanalytical Chemistry, 2004.
______________

Finite element simulation of Off-Gel buffering.
Isabelle Arnaud, J. Josserand, J. S. Rossier, and H. H. Girault - Electrophoresis, volume 23, 2002.
______________
© Laboratoire d'Electrochimie Physique et Analytique (LEPA) - EPFL